
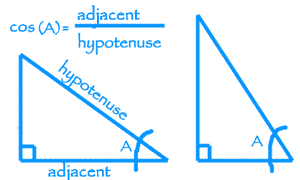
This more general and abstract treatment not only reveals the equivalence of the two definitions but also provides an instructive perspective on circular and harmonic motion as studied in kinematics. We start with the usual length projections on the unit circle and use elementary geometry and elementary calculus to arrive to harmonic differential equations. Law of cosines c2a2+b2-2abcos (gamma) c2 a2 +b2 2abcos() Want to learn more about the law of sines Check out this video. Thus, cosine of an angle, in a right-triangle, is equal to the ratio of adjacent side of that angle and hypotenuse of the triangle. This angle is an acute angle in a right angled triangle, which is considered to find the ratios. In this case, the dot product is used for defining lengths (the length of a vector is the square root of the dot product of the vector by itself) and angles (the cosine of the angle between two. The cos meaning in trigonometry defines the cosine of an angle. In modern geometry, Euclidean spaces are often defined by using vector spaces. In this manuscript, the equivalence between the geometrical and the differential definition is presented assuming no a priori knowledge of the properties of sine and cosine functions. These definitions are equivalent when using Cartesian coordinates.
Although the two definitions must be equivalent, this equivalence is not demonstrated in textbooks.

These two forms correspond to two different definitions of trigonometric functions, one geometrical using right triangles and unit circles, and the other employing differential equations.
COSINE GEOMETRY DEFINITION PDF
Petrache Download PDF Abstract:In classical physics, the familiar sine and cosine functions appear in two forms: (1) geometrical, in the treatment of vectors such as forces and velocities, and (2) differential, as solutions of oscillation and wave equations. Spherical trigonometry is of great importance for calculations in astronomy, geodesy, and. On the sphere, geodesics are great circles. Download a PDF of the paper titled Correspondence between geometrical and differential definitions of the sine and cosine functions and connection with kinematics, by Horia I. Spherical trigonometry is the branch of spherical geometry that deals with the metrical relationships between the sides and angles of spherical triangles, traditionally expressed using trigonometric functions.


 0 kommentar(er)
0 kommentar(er)
